Introduction
If we’re going to build a computer, we’ll have to be able to perform some boolean arithmetic. This post is dedicated to the creation of four “chips” that do just that, though all of them perform only addition is some way.
The Chips
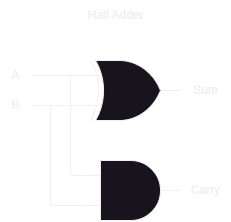
Half Adder
The “Half Adder” adds two bits together and produces a sum bit and a carry bit, just like in regular long addition. It’s called a “Half Adder” because while it produces a carry bit, it does not accept a carry bit as an input (which may have come from a previous addition).
| A | B | Sum | Carry |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
If we examine where the outputs are 1 in the table, we can produce the following boolean equations
The Sum should look familiar: It’s the boolean equation for an XOR gate (see Project 1 if you don’t remember). The Carry should be even easier, as it’s just an AND gate.
CHIP HalfAdder {
IN a, b; // 1-bit inputs
OUT sum, // Right bit of a + b
carry; // Left bit of a + b
PARTS:
And (a=a, b=b, out=carry);
Xor (a=a, b=b, out=sum);
}Full Adder
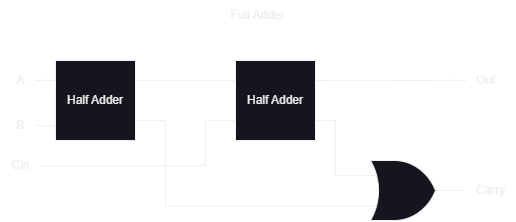
The purpose of a “Full Adder” is to add 3 bits: Two bits from the current operation, and a carry bit from a previous addition (Cin which stands for “Carry in”).
| A | B | Cin | Sum | Carry |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
While we could make boolean equations, like in the Half Adder implementation, another approach is used instead: Two Half Adders and an OR gate.
How does this work? Let’s look at two scenarios: When A=0, B=1 and when A=B=1. We’ll let Cin=1.
Scenario 1
- Let
A=0,B=1 sum=1,carry=0for the first Half AdderInput1=sum=1,Input2=Cin=1for the second Half Addersum=0,carry=1for the second Half Adderout=0,carry=1for the Full Adder
Scenario 2
- Let
A=B=1 sum=0,carry=1for the first Half AdderInput1=sum=0,Input2=Cin=1for the second Half Adderout=1,carry=0for the second Half Adderout=1,carry=1for the Full Adder
In scenario 1, the second Half Adder produced a carry bit.
In scenario 2, the first Half Adder produced a carry bit.
Since we simply can’t discard the carry bit (it could be used in a future Full Adder Cin bit), we OR the two carry’s from the Half Adders to produce the carry bit for the Full Adder. Also note that only one of the Half Adders will produce a carry bit.
One may wonder, why don’t we put the carry bit from the first Half Adder into the second Half Adder? This is because, as mentioned before, we’re actually adding just 3 bits: the two current numbers A and B, and a carry from a previous addition (Cin). Any carry’s produced from our operations here will be sent to the next Full Adder.
CHIP FullAdder {
IN a, b, c; // 1-bit inputs
OUT sum, // Right bit of a + b + c
carry; // Left bit of a + b + c
PARTS:
HalfAdder (a=a, b=b, sum=s1, carry=c1);
HalfAdder (a=s1, b=c, sum=sum, carry=c2);
Or (a=c1, b=c2, out=carry);
}Add16
This is straightforward: add two 16-bit numbers together.
Note
- The first Full Adder could have been replaced with a Half Adder
AandBare added bitwise, but thecarrys are fed into the next Full Adder
It should be noted that the method used to add the numbers is called a “Ripple Adder” and it isn’t the most efficient. A better adder is called a “Carry Look-Ahead” adder.
CHIP Add16 {
IN a[16], b[16];
OUT out[16];
PARTS:
FullAdder (a=a[0], b=b[0], c=false, sum=out[0], carry=c0);
FullAdder (a=a[1], b=b[1], c=c0, sum=out[1], carry=c1);
FullAdder (a=a[2], b=b[2], c=c1, sum=out[2], carry=c2);
FullAdder (a=a[3], b=b[3], c=c2, sum=out[3], carry=c3);
FullAdder (a=a[4], b=b[4], c=c3, sum=out[4], carry=c4);
FullAdder (a=a[5], b=b[5], c=c4, sum=out[5], carry=c5);
FullAdder (a=a[6], b=b[6], c=c5, sum=out[6], carry=c6);
FullAdder (a=a[7], b=b[7], c=c6, sum=out[7], carry=c7);
FullAdder (a=a[8], b=b[8], c=c7, sum=out[8], carry=c8);
FullAdder (a=a[9], b=b[9], c=c8, sum=out[9], carry=c9);
FullAdder (a=a[10], b=b[10], c=c9, sum=out[10], carry=c10);
FullAdder (a=a[11], b=b[11], c=c10, sum=out[11], carry=c11);
FullAdder (a=a[12], b=b[12], c=c11, sum=out[12], carry=c12);
FullAdder (a=a[13], b=b[13], c=c12, sum=out[13], carry=c13);
FullAdder (a=a[14], b=b[14], c=c13, sum=out[14], carry=c14);
FullAdder (a=a[15], b=b[15], c=c14, sum=out[15], carry=ignore);
}Inc16
This one is simple. Inc16 just increments the given number, in, by 1. We let a=in and b[0]=1. This gets us out=a+b which is the same as out=in+1.
CHIP Inc16 {
IN in[16];
OUT out[16];
PARTS:
Add16 (a=in, b[0]=true, b[1..15]=false, out=out);
}