Project Euler

Problem

This problem comes from Project Euler 18

Problem

By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23.

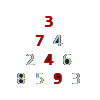
That is, 3 + 7 + 4 + 9 = 23.

Find the maximum total from top to bottom of the triangle below:

NOTE: As there are only 16384 routes, it is possible to solve this problem by trying every route. However, Problem 67, is the same challenge with a triangle containing one-hundred rows; it cannot be solved by brute force, and requires a clever method! ;o)

Solution

It’s easier to solve the problem by starting at the bottom and working towards the top. This allows us to have just one number at the end instead of a row of numbers.

They say “a picture is worth a thousand words,” so here’s an animation of what the code will do.

The code looks at two adjacent numbers in a lower row and adds whichever is greater to the number above them. You may have to watch the animation a few times to get it, but this explains what’s going on far better than any words I can say.

Code

# Project Euler: Problem 18
# Maximum path sum I

a = [
    [75],
    [95, 64],
    [17, 47, 82],
    [18, 35, 87, 10],
    [20, 4, 82, 47, 65],
    [19, 1, 23, 75, 3, 34],
    [88, 2, 77, 73, 7, 63, 67],
    [99, 65, 4, 28, 6, 16, 70, 92],
    [41, 41, 26, 56, 83, 40, 80, 70, 33],
    [41, 48, 72, 33, 47, 32, 37, 16, 94, 29],
    [53, 71, 44, 65, 25, 43, 91, 52, 97, 51, 14],
    [70, 11, 33, 28, 77, 73, 17, 78, 39, 68, 17, 57],
    [91, 71, 52, 38, 17, 14, 91, 43, 58, 50, 27, 29, 48],
    [63, 66, 4, 68, 89, 53, 67, 30, 73, 16, 69, 87, 40, 31],
    [4, 62, 98, 27, 23, 9, 70, 98, 73, 93, 38, 53, 60, 4, 23]
]

rows = len(a)-1
for x in range(rows, -1, -1):
    columns = len(a[x])-1
    for y in range(columns):
        if(a[x][y] > a[x][y+1]):
            a[x-1][y] += a[x][y]
        else:
            a[x-1][y] += a[x][y+1]

print(a[0])

Note

I use x and y in the code above for coordinates for the 2D array a in the form a[x][y].

• x is a row such as a[2] = [17, 47, 82] and,
  
• y is a column of that row such as a[2][0] = 17.